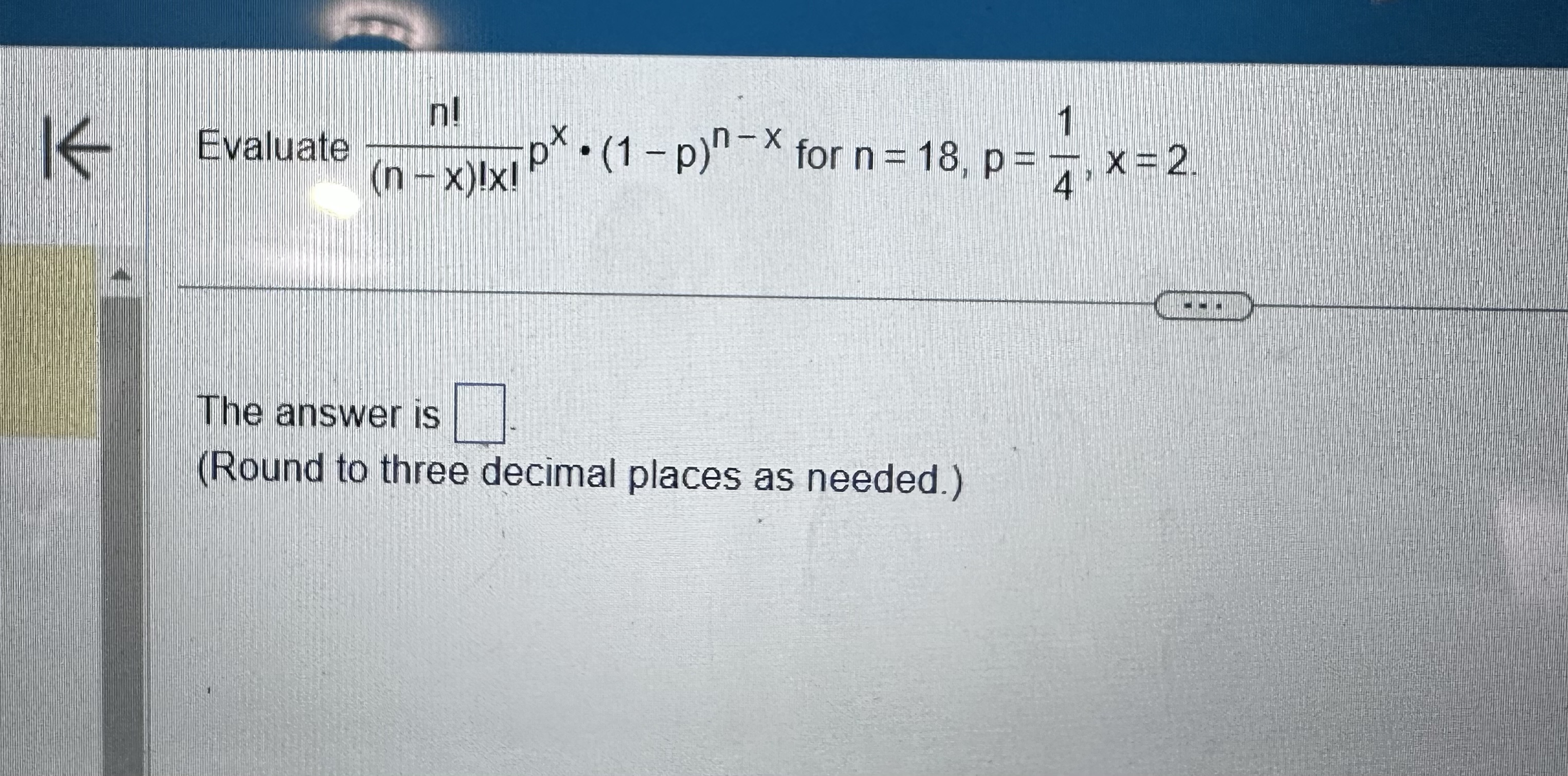
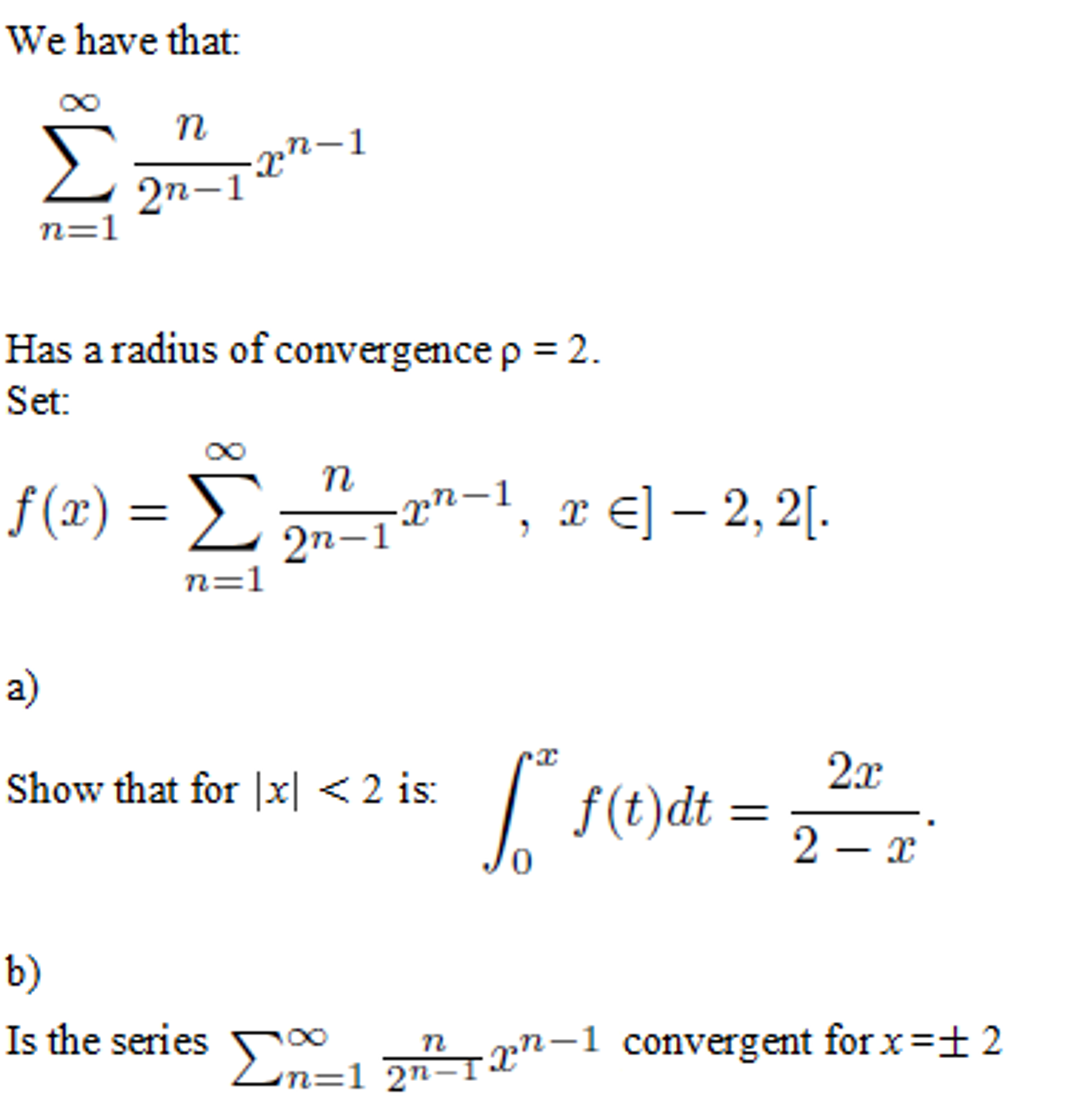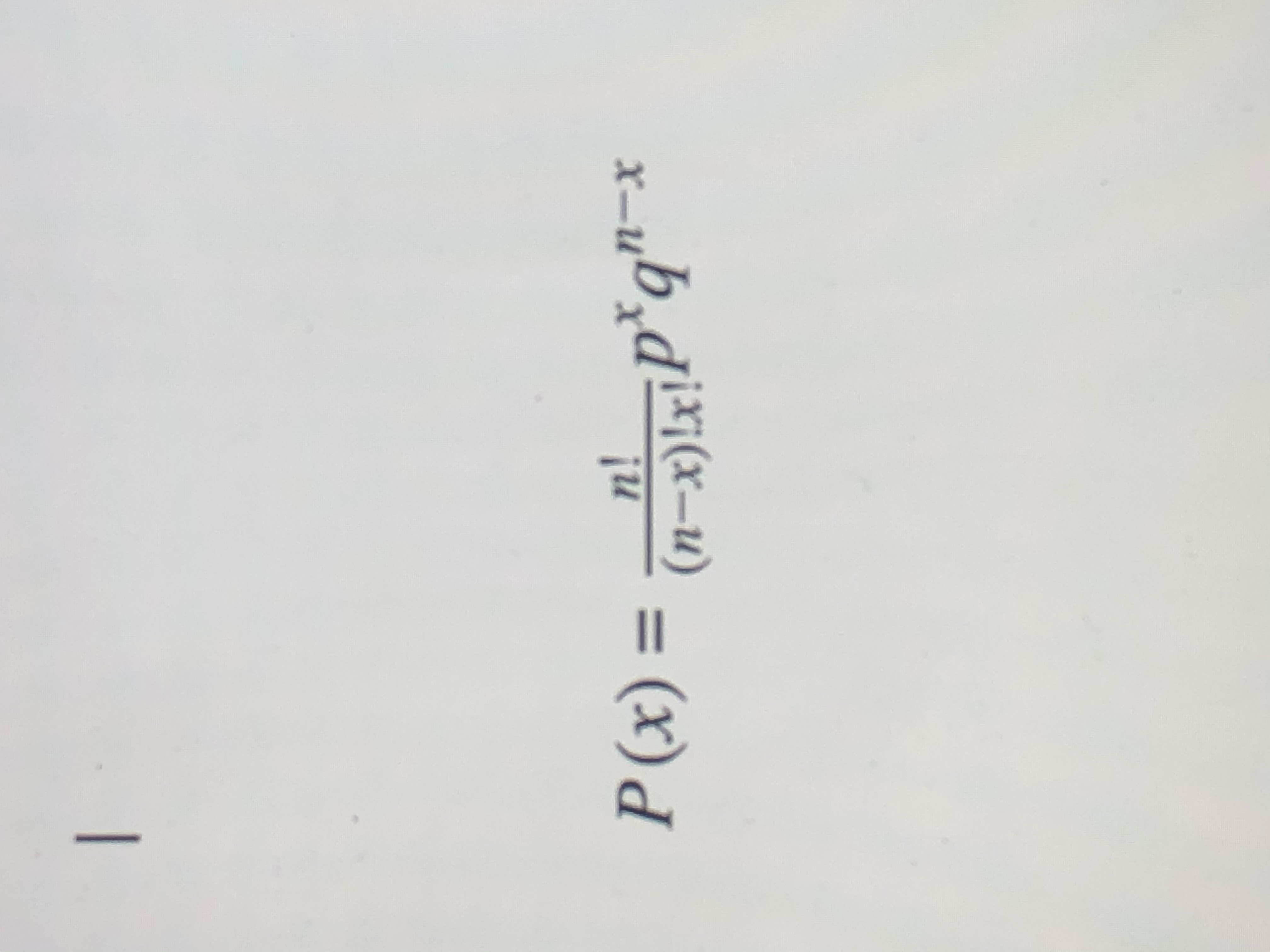Webthe power rule is used to differentiate the algebraic expressions of the form x^n. Webfirst remark that the polynomial x^m+k has simple roots. Let us call the roots c_j for 1\leq j\leq m. Therefore x^n/(x^m+k) rewrites as a sum of simple elements. Webwhat is the derivative of xn? For the function f (x) = xn, n should not equal 0, for reasons which will become clear. Product of exponentials with same base. If we take the product of two exponentials with the same base, we simply add the exponents: Xaxb = xa + b. Webusing the ratio test, $\dfrac{a_{n+1}}{a_n} = \dfrac{(n+1)x^{n+1}}{nx^n} = \dfrac{(n+1)x}{n}$. So, the series converges when $|x| $$f(x) = \sum_{n=1}^\infty n.
Recent Post
- Honeysuckle Tattootypography
- Tractor Supply Burgaw Nc
- Ryan Taugher Nashvilletimeline Photos
- Limestone Funeral Home Athens Al
- Nickelodeon Animated Shows 2000s
- Michaelscrafts
- Death Of A Twin Flame
- Best Careers Without Degree
- Smith Funeral Home Monroe Obituarieslibrary
- Collier County Arrests Mugshotsshop
- Rchainsawman
- Bju Press Homeschoolindex2
- Sean Sobotka Obituaryindex
- Irs Refund Reddit 2024shop Cart
- Dunn Funeral Home Bristol Obituariesredpit
Trending Keywords
- Cna Agencyfav Page Create
- Spectrum Outage Tampa Flregister
- Daley Murphy Wisch Funeral Home Beloitforum Open Topic
- Worley Funeral Home Clintonlogout
- Honeysuckle Tattootypography
- Tractor Supply Burgaw Nc
- Ryan Taugher Nashvilletimeline Photos
- Limestone Funeral Home Athens Al
- Nickelodeon Animated Shows 2000s
- Michaelscrafts
Recent Search
- Usps Locatorpittube Category
- Ups Print Paperfav Page
- Mailing Address For Comcast Paymentsabout
- Samantha Hyden Cause Of Death
- Washington Evening Journal Washington Ia Obituariesforum Open Topic
- Cc Caller Times Obit
- Rt 9 Crashpost Versions
- Criminal Minds Fanfiction Reidforum Open Topic
- Arrest Oconee County Sctimeline Friends2
- Cash Paying Jobs Near Mesetting
- Sephora Pay Rate
- Hollier Reviewforum Open Topic
- Cna Agencyfav Page Create
- Spectrum Outage Tampa Flregister
- Daley Murphy Wisch Funeral Home Beloitforum Open Topic